Multi-objective Racing Algorithm

Model selection is an important aspect of Machine Learning (ML). Aside from its traditional meaning, occasionally a “model” could also refer to any algorithm or learning strategy. Given an ensemble of candidate models, each model’s performance is assessed on a common set of test instances and, eventually, based on their performance on the aforementioned test, a single champion model or a subset of the ensemble is identified as the best for the given ML task. Typically, the larger the cardinality of the test instance set, the more confidence can be bestowed on the final choice(s). However, as the number of test instances and models to be compared increases, model selection becomes a time-consuming task.

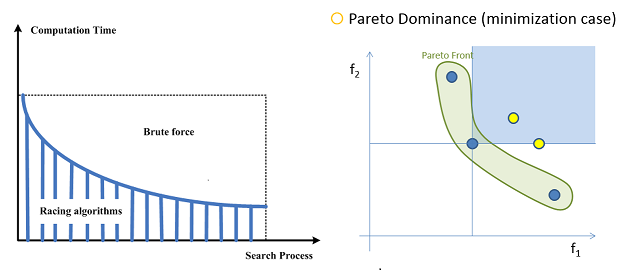
Alternatively, one may be willing to trade off some computational complexity for a somewhat reduced, but still acceptable, likelihood that the models obtained from a suitably modified selection process are indeed the ones that outperform the rest of the ensemble. The goal of RAs is to automatically detect under-performing models and exclude them from further consideration as early as possible during the race in order to save on computations. This very notion forms the main premise of Racing Algorithms (RAs), which have been widely used in parameter tuning, automatic model configuration, algorithm development and industrial applications.

So far, all existing RAs consider a single measure of goodness. However, in real-life problems, model selection often involves employing more than one quantifiable selection criterion.  For example, as less complex models (e.g. with fewer parameters) may exhibit better generalization performance (or, plainly, be preferred to) than more complex ones. Model complexity could or should be considered in addition to prediction accuracy. Furthermore, in a Multi-Task Learning context, models with multiple outputs are considered to simultaneously serve more than one tasks (each output is dedicated to a specific task). In such a scenario, the performance quality for each task is linked to a different objective function and the model selection problem becomes one of multi-objective nature.

Therefore, in paper [1], we proposed a novel Multi-Objective RA procedure, namely S-Race. Its purpose is to yield the subset of the candidate ensemble, whose models are non-dominated in the Pareto sense with respect to the remainder of the ensemble, when all objectives are taken into account simultaneously.  At the highest level, the step-wise S-Race employs testing the significance of simultaneous dominance relationships that may be observed between families of candidate models. Strong Type I control of these simultaneous formal tests is achieved by the Holm’s Step-Down procedure. At a lower level, probabilistic dominance relationships between individual pairs of models are inferred based on the Sign Test for matched-pair comparisons.