Metric Learning

Many Machine Learning algorithms entail the computation of distances, for example, k-nearest neighbor (KNN) for classification and k-Means for clustering. In most cases, when computing distances, the Euclidean distance metric is employed. However, the use of fixed distance metric may not necessarily perform well for all problems. Research Attention was directed to data-driven approaches in order to infer the best metric for a given problem. This technique is referred to as Metric Learning.

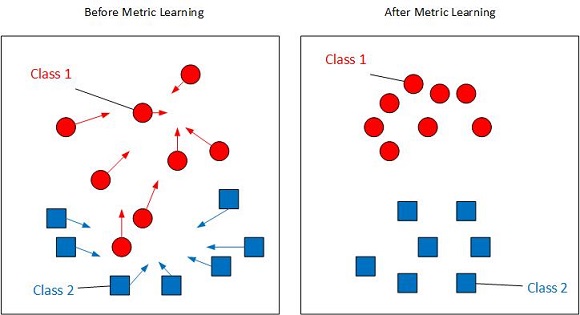
A typical instance of Metric Learning is the learning of the weight matrix that determines the Mahalanobis metric, with the assistance of pair-wise sample similarity information. The goal of Metric Learning is to map similar samples close together and to map dissimilar samples far apart as measured by the learned metric. As shown in the image, red circles and blue squares are different classes. After learning the metric, similar samples (red circles or blue squares) are mapped closer while dissimilar samples are far apart.

Most of the Metric Learning is the use of a single, global metric, i.e., a metric that is used for all distance computations. This scenario may not be well-suited in some settings. We propose a new local metric learning approach, which we will refer to as Reduced-Rank Local Metric Learning (R2LML). Local metric here means our model learns several metrics that take into account the location and similarity of the data involved. The details of R2LML can be found in our published paper [2] in ECML/PKDD 2013. We also provide the Matlab code for this model in [1]. In another work [3], the data points are first mapped to a so-called Output Space via a non-linear function. Then, a distance metric is learned in the output space.